Introduction 
Matrix Action 
Perpframes, 
Aligners and Hangers 
Stretchers 
Coordinates 
Projections 
SVD 
Matrix Subspaces  
Linear Systems 
Pseudo-Inverse 
Condition Number 
Matrix Norm 
Rank One 
Data Compression 
Noise Filtering 
Todd Will
UW-La Crosse
  2D Perpframes 
3D Perpframes 
Aligners

Perpframes,
Aligner and Hangers

  Hangers 
Hitting 
Exercises

2D perpframes

In 2D you need to perpendicular unit vectors to form a perpframe. 

One way to get a perpframe is to specify an angle s and use the vectors 

[Graphics:textgr1.gif] and [Graphics:textgr2.gif] .



Here are perpframes for some choices of s. 

 

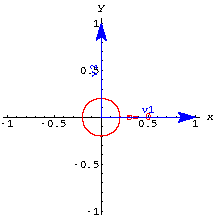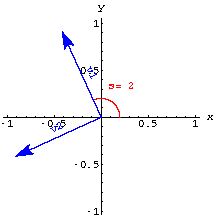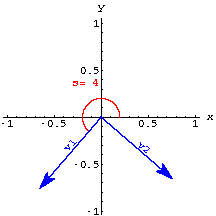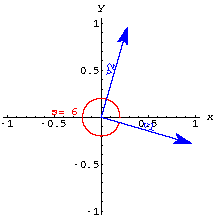
3D perpframes

A 3D perpframe consists of three mutually perpendicular unit vectors. 

Coming up with a 3D perpframe is a little trickier, but you can look at some examples in the plot below. 

 
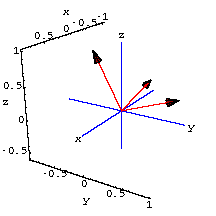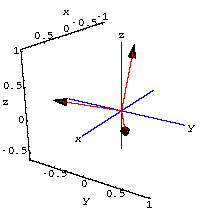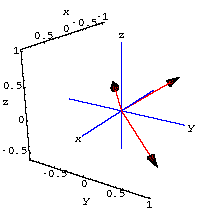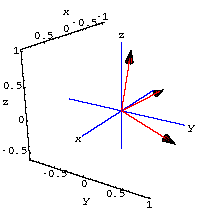
Lots of folks call perpframes by the name "orthonormal basis". 

Aligners

You get an aligner matrix by loading the vectors from a perpframe into the rows of the matrix. 

[Graphics:textgr3.gif] 

The perpframe below consists of [Graphics:textgr5.gif] and [Graphics:textgr6.gif]. 

The aligner matrix you get from this perpframe is [Graphics:textgr7.gif]. 


 


Mouse over the plot to check out the action of this aligner matrix on the unit circle. 

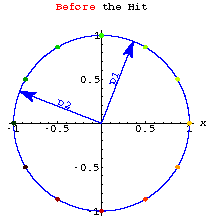
The aligner matrix gets its name since it aligns the perpframe to the xy-axis. 



Specifically the aligner matrix [Graphics:textgr8.gif] sends  to [Graphics:textgr10.gif] and sends  to [Graphics:textgr12.gif]. 

You can verify this by hand 

[Graphics:textgr13.gif] 

[Graphics:textgr14.gif] 

(1) uses the row way to multiply a matrix times a vector. 

(2) since  and  are a perpframe [Graphics:textgr17.gif] and [Graphics:textgr18.gif]. 

Hangers

You get a hanger matrix by loading the vectors from a perpframe into the columns of the matrix. 

[Graphics:textgr19.gif] 

Stay with the same perpframe from above [Graphics:textgr20.gif] and [Graphics:textgr21.gif]. 

The hanger matrix you get from this perpframe is [Graphics:textgr22.gif]. 

 

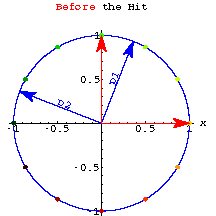
Mouse over the plot to check out the action of this hanger matrix on the unit circle. 

The hanger matrix gets its name since it hangs the xy-axis onto the perpframe. 

Specifically the hanger matrix [Graphics:textgr23.gif] sends[Graphics:textgr24.gif] to  and sends [Graphics:textgr26.gif] to . 

You can verify this by hand 

[Graphics:textgr28.gif] 

(1) This is the COLUMN WAY to multiply a matrix times a vector. 

Hitting curves with aligners and hangers.

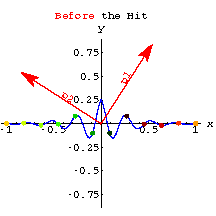
The plot shows the perpframe ,  and a damped sine curve lined up on the xy-axis. 

See what happens when you hit the curve with the hanger matrix [Graphics:textgr31.gif]. 

  
The hanger matrix hangs the curve on the perpframe. 

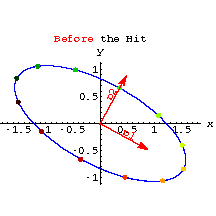
The next plot shows an ellipse skewered on the perpframe , . 

See what happens when you hit the ellipse with the aligner matrix [Graphics:textgr34.gif]. 

 
The aligner matrix aligns the ellipse on the xy-axis. 

Exercises

1. The plot shows a bell skewered on a red 3D perpframe consisting of the vectors , , [Graphics:textgr37.gif]. 

Mouse over the plot to see the action of a certain matrix A. 

 
 
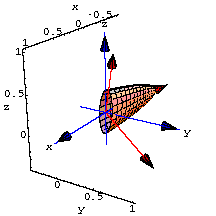
Based on the action, the matrix A seems to be (choose one): 

(a) the aligner matrix =[Graphics:textgr38.gif] 

(b) the hanger matrix = [Graphics:textgr39.gif] 

2. The plot shows a red 3D perpframe consisting of the vectors , , [Graphics:textgr42.gif] and a bell. 

Mouse over the plot to see the action of a certain matrix A. 

 
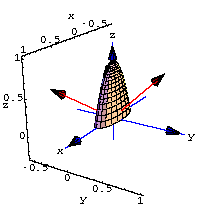
Based on the action, the matrix A seems to be (choose one): 

(a) the aligner matrix = [Graphics:textgr43.gif] 

(b) the hanger matrix = [Graphics:textgr44.gif] 
 
© 1999 Todd Will
Last Modified: 05-Jan-1999
Hit Counter