SVD

Matrix Norm, Rank One

Data Compression

Noise Filtering

Todd Will
UW-La Crosse

Two-thirds Theorem

Good Basis Theorem

SVD

Exercises

Singular Value Decomposition

The singular value decomposition for a matrix A writes A as a product (hanger)(stretcher)(aligner).

It's an amazing and useful fact that every m x n matrix has a singular value decomposition.

The following theorem goes two-thirds of the way to proving this fact:

Two-thirds Theorem

For an

matrix

and any orthonormal basis

define

and

[Graphics:svdgr6.gif] .

Then [Graphics:svdgr7.gif] .

Proof: Using first the row way and then the column way to multiply a matrix times a point, you see that the right hand side of the equation sends to .

Thus the two sides of the equation agree on the basis and so must be equal.

The two-thirds theorem gets you two-thirds of the way to the SVD.

It says that given any orthonormal basis of you can write

So you've got the stretcher and the aligner -- if were a hanger matrix then this would be a Singular Value Decomposition for A.

For to be a hanger matrix requires that the columns be pairwise perpendicular.

So one challenge to finding an SVD for A is to find an orthonormal basis of , so that for all , .

Theorem: If A is an m x n matrix, then there is an orthonormal basis of , so that for all , .

Proof 1: For matrices

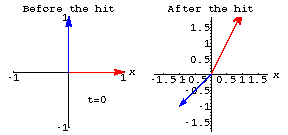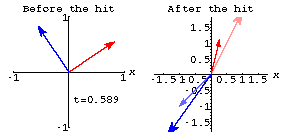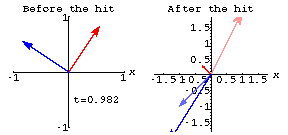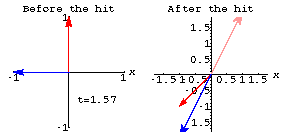
You can get 2D perpframes using

and specifying an angle

You'd like to show that for any m x 2 matrix there's an angle t so that
is zero.

How do you know there is always such a ?

Answer: Go with the example matrix and look at the following plot that shows the perpframe and before and after the hit with A.

Notice that when

, the angle between

and

is greater than

By the time , the angle is less than .

That's enough to guarantee that somewhere between and there's an angle where and are perpendicular.

Most reasonable folks would accept the evidence given in the plots, but the doubters might want to look at the function:

Then

(1) The definition of f.

(2) Linearity of matrix hits.

(3) The definition of f.

This equation says that and have opposite signs. This should convince even the doubters that there's a between and that makes zero.

The same argument holds for any m by 2 matrix.

Proof 2: General case

The proof above works well enough for m x 2 matrices, but this proof shows that for all m x n matrices there's is a perpendicular frame

of unit vectors so that

for

Here's one way to get such a perpframe.

Start with a m x n matrix A.

Step 1: Let be a unit vector maximizing .

Step 2: Let be the space perpendicular to
Let be a unit vector in maximizing .

Step 3: Let be the space perpendicular to
Let be a unit vector in maximizing .
.
.
.
Step n: Let be the space perpendicular to
Let be a unit vector in maximizing .

This gets you a perpendicular frame of unit vectors , but how do you know that for ?

Look at and see that

no matter what you choose is a unit vector in
.

Since is a unit vector in maximizing and is in for all , you know that has a maximum at .

This tells you .

Now compute:

When you remember , , and are just numbers, you understand that its nothing more than tedious to compute:

Plugging in gives you .

But you already know that , so after canceling the you get which is just what you wanted.

Proof 3: Based on the spectral theorem

This proof is slick IF YOU'VE ALREADY SEEN THE SPECTRAL THEOREM.

If you haven't seen the spectral theorem, then skip this proof.

Given and an orthonormal basis of ,

iff

iff are all eigenvectors of .

Conclusion: The desired basis is guaranteed by spectral theorem since is symmetric.

Theorem: Every matrix has a singular value decomposition.

The theorem above almost gives you the SVD for any matrix.

The only problem is that although the columns of the "hanger" matrix are pairwise perpendicular, they might not form a basis for .

For example, suppose for a 5x4 matrix the procedure outlined above gives you:

To complete the decomposition, let be an orthonormal basis for the three dimensional subspace of perpendicular to .

Then write

(1) The two sides agree on the basis

This, finally, is a singular value decomposition for A.

Comments:

The diagonal entries of the stretcher matrix are called the "singular values of A".

An extra row of zeros has been added to the stretcher matrix to produce the dimensions required for the multiplication. If A is m x n with , then rows will be deleted.

In either case, the dimensions of the stretcher matrix will always match the dimensions of A.

The decomposition shows that the action of every matrix can be described as a rotation followed by a stretch followed by another rotation.

The proofs above are meant to show that every matrix has an SVD. You can compute SVD's for mx2 matrices by hand, but you should use a machine to compute SVD's for bigger matrices.