Todd Will
UW-La Crosse

Matrix Subspaces

What's the pay off? 

Fundamental equations

2x2 Example

 

 

Now watch what the matrix A does to an ellipse lined up on the perpframe . 

 

 

 

The matrix stretches the ellipse and transfers it from the  perpframe to the  perpframe. 
 

If you look carefully at the "during" plot you'll see that A sends  to  and  to . 
 

More generally A, 
 

• stretches vectors parallel to  by a factor of 3 and rotates them in the direction of ,
• stretches vectors parallel to  by a factor of  and rotates them in the direction of . 

You can verify this by computing what each factor of A does. 

Check what each factor of A does to : 

(The aligner matrix brings  to the y-axis.) 

(The stretcher matrix stretches the y-axis by a factor of .) 

(The hanger rotates the y-axis to the direction of .) 

Theorem:

• a 2D perpframe  for your ,

 
• a 2D perpframe  for your ,

 
• numbers  and  for your stretcher . 

These two equations are the fundamental equations of matrices of the form (hanger)(stretcher)(aligner). 
 

In words they say that A 

• stretches vectors in the direction of  by a factor of  and rotates them to the direction of , 
• stretches vectors in the direction of  by a factor of  and rotates them to the direction of . 

Proof: Outlined above--follow the action of each factor of A on . 

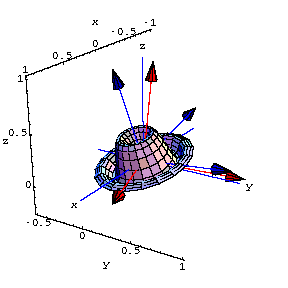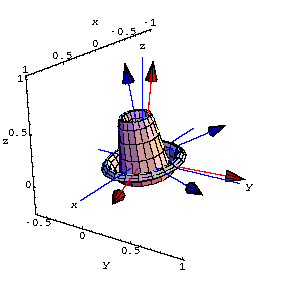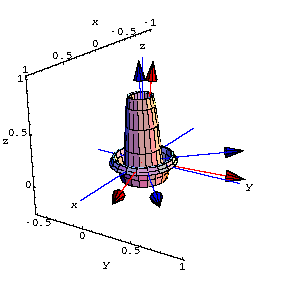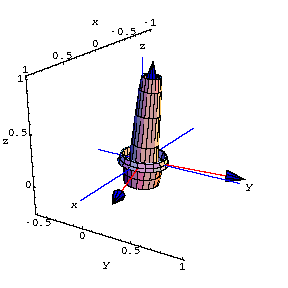
3 x 3 matrices.

Just as in the 2x2 case, the matrix A obeys the fundamental equations:  

In fact, matrices of the form (hanger)(stretcher)(aligner) always obey these fundamental equations, regardless of their dimension. 

Orthonormal bases for fundamental subspaces.

Proofs:

              (The column way to multiply A v.)
 

     (Since the a's are a basis.)
 

      (Linearity)
 

          (Fundamental Equations)
 

. 

This shows shows that Col[A] = span. 

Since  are perpendicular unit vectors they are an orthonormal basis for Col[A]. 

The nullspace of A, N[A], is the set of vector that A sends to the zero vector. 
 

Suppose . 
 

Then  
 

                     (Linearity and Fundamental Equations.)
 

. 

Now,  tells you that  and so . 
 

This tells you that any vector in N[A] is a linear combination of  and , i.e. . 

On the other hand, , so . 
 
 

The row space of A is the span of the rows of A, which is the same as the column space of . 

So finding a basis for the row space of A is the same as finding a basis for the columns space of . 
 
 

Here's a look at : 

Now you have  written as (hanger)(stretcher)(aligner), 

                               i.e., you have an SVD of . 
 

So from what you did above you know 

•   is an orthonormal basis for the , 

 
• is an orthonormal basis for . 

Comments

• the columns of the hanger matrix corresponding to non-zero singular values are an orthonormal basis for Col[A]. 

 
• the rows of the aligner matrix corresponding to non-zero singular values are an orthonormal basis for Row[A]. 

 
• the rows of the aligner matrix corresponding to zero singular values are an orthonormal basis for N[A].

 
• the columns of the hanger matrix corresponding to zero singular values are an orthonormal basis for .

Bonus Facts.

Definitions:

Since the columns of the hanger matrix corresponding to non-zero singular values form a basis for the column space, you know that the rank of A is equal to the number of non-zero singular values.
 

Similarly, since the nullity of A is the dimension of the null space, the number of zero singular values equals the nullity of A. 

Theorem: rank[A]+nullity[A] 

Theorem:  

(1) Since the stretcher matrix for  is the transpose of the stretcher matrix for A, the singular values for A and  are identical. 
 

Exercises

give orthonormal bases for 

a. the column space of A 

b. the row space of A 

c. the nullspace of A 

d. the nullspace of . 

2. Let .     Here is an SVD for A. 

Based on the SVD, give an orthonormal basis for the subspace spanned by  

3. Let . Here is an SVD for A. 

Based on the SVD of A and the fundamental equations, compute 

a.  

b.  

If you check your answer by using , you may not get agreement since the SVD for A has been rounded to two decimals.