Introduction 
Matrix Action 
Perpframes, Aligners and Hangers 
Stretchers 
Coordinates 
Projections 
SVD 
Matrix Subspaces  
Linear Systems, Pseudo-Inverse 
Condition Number 
Matrix Norm, Rank One 
Data Compression 
Noise Filtering 
Todd Will
UW-La Crosse
  Stretchers 
More Stretchers 

Stretchers

 Changing Dimensions 
Exercises

Stretchers

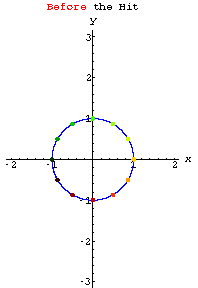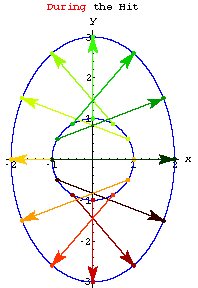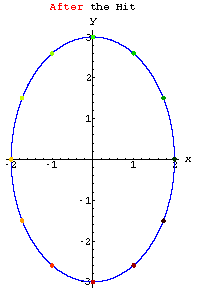
Look at the action of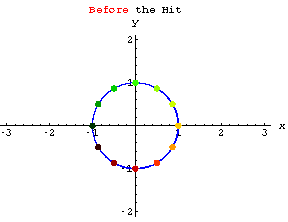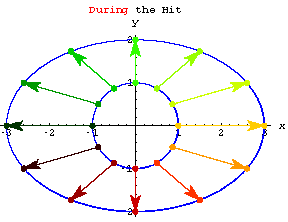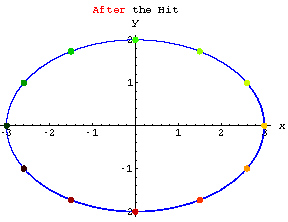 [Graphics:stretchergr1.gif]. 
 
 
 
 

When you look at that action you can see why it's natural to call a diagonal matrix a "stretcher" matrix. 

The diagonal matrix [Graphics:stretchergr6.gif] stretches in the x direction by a factor of "a" and in the y direction by a factor of "b". 

You can verify this by hand using the column way to multiply a matrix times a vector: 

[Graphics:stretchergr7.gif] 

Check out a few more stretchers.

[Graphics:stretchergr8.gif] 

Stretching by 1/2 squashes the circle in the y direction. 


   
[Graphics:stretchergr12.gif]
 
 
 
Stretching by 0 in the y direction squashes the circle onto the x-axis. 

[Graphics:stretchergr16.gif]
 
 
 
Stretching by -2 in the x-direction, means flipping across the y-axis as well as stretching. 

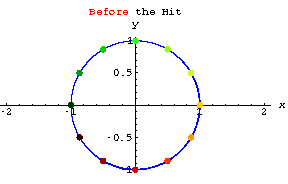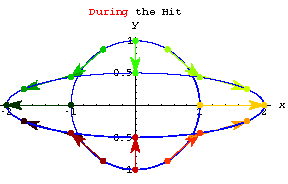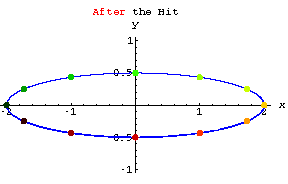
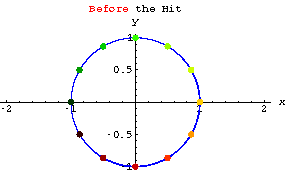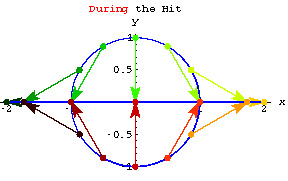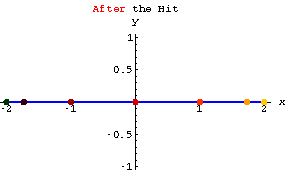
Changing dimensions

Both [Graphics:stretchergr21.gif]and [Graphics:stretchergr22.gif]are stretcher matrices since their non-diagonal entries are zero. 

The matrix [Graphics:stretchergr23.gif] sends [Graphics:stretchergr24.gif]to [Graphics:stretchergr25.gif]. 
 

But[Graphics:stretchergr26.gif]sends [Graphics:stretchergr27.gif]to [Graphics:stretchergr28.gif]. 
 
 

Check out the action of each of these stretchers. 
  

[Graphics:stretchergr29.gif]
 
 
 
A stretch by a factor of 5 in the x direction and a factor of 2 in the y direction. 

[Graphics:stretchergr33.gif]
A stretch by a factor of 5 in the x direction and a factor of 2 in the y direction. 

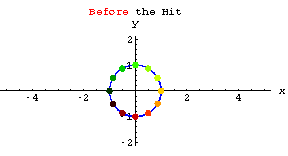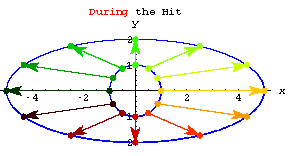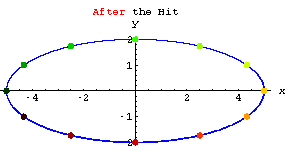
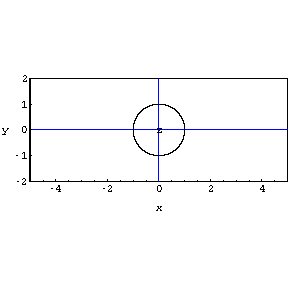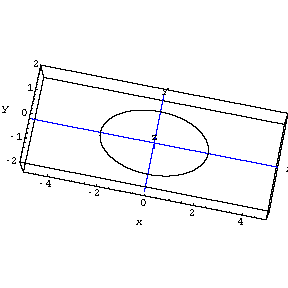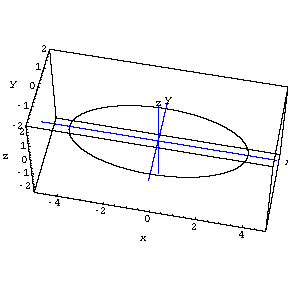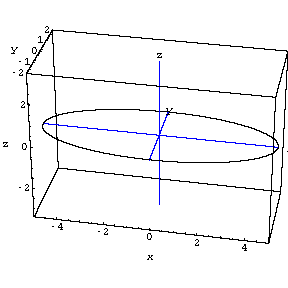
But note how the stretcher matrix [Graphics:stretchergr34.gif]not only stretches the 2D circle but also embeds the ellipse into 3 dimensional space. 

Exercises

1.  Check out the following ellipse.  
[Graphics:stretchergr35.gif]
[Graphics:stretchergr36.gif] 

You can get this ellipse by stretching the unit circle by a factor of 3 in the x direction and a factor of 2 in the y direction. 

To get the ellipse shown above I would hit the unit circle with (choose one): 


(a) the matrix [Graphics:stretchergr37.gif] 


(b) the matrix [Graphics:stretchergr38.gif] 


(c) the matrix [Graphics:stretchergr39.gif] 

2.  Check out the following ellipsoid  

[Graphics:stretchergr40.gif]
[Graphics:stretchergr41.gif] 

You can get this ellipsoid by stretching the unit sphere by 

  • a factor of 4 in the x direction 
  • a factor of 8 in the y direction
  • a factor of 2 in the z direction
To get the ellipsoid shown above I would hit the unit sphere with (choose one): 

(a) the matrix [Graphics:stretchergr42.gif] 

(b) the matrix [Graphics:stretchergr43.gif] 

(c) the matrix [Graphics:stretchergr44.gif] 

© 1999 Todd Will
Last Modified: 07-Jan-1999
Hit Counter